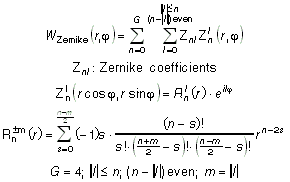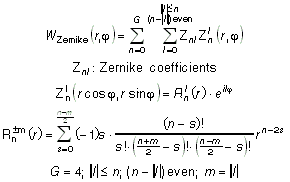Polinômios de Zernike
Os polinômios de Zernike representam um método muito
usado em óptica para descrever aberrações de frentes
de onda.
Os polinômios de Zernike WZernike(r,j) de
4th grau podem ser escritos como:
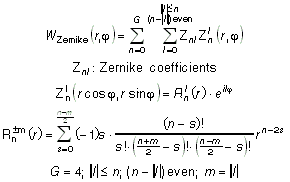
O significado dos polinômios de Zernike normalizados (Noll
1976) e seus coeficientes podem ser vistos na
Tab. 1
e Tab. 2:
|
j
|
n
|
l
|
Zln(r,j)
|
Significado
|
Dj
|
Dj - Dj-1
|
|
1
|
0
|
0
|
1
|
Constante (Bias)
|
1.030 S
|
|
|
2
|
1
|
1
|
2r cos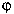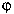 
|
Tilt (direção y)
|
0.582 S
|
0.448 S
|
|
3
|
1
|
-1
|
2r sin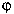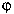
|
Tilt (direção x)
|
0.134 S
|
0.448 S
|
|
4
|
2
|
0
|
31/2 (2r2
- 1)
|
Defocus
|
0.111 S
|
0.023 S
|
|
5
|
2
|
2
|
61/2 r2
sin 2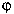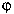
|
Astigmatismo 1a ord. 45°
|
0.0880 S
|
0.023 S
|
|
6
|
2
|
-2
|
61/2 r2
cos 2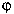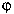
|
Astigmatismo 1a ord. 0°
|
0.0648 S
|
0.023 S
|
|
7
|
3
|
1
|
81/2 (3r3
- 2r) sin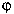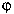
|
Coma (direção y)
|
0.0587 S
|
0.0062 S
|
|
8
|
3
|
-1
|
81/2 (3r3
- 2r) cos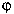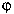
|
Coma (direção x)
|
0.0525 S
|
0.0062 S
|
|
9
|
3
|
3
|
81/2 r3
sin 3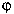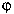
|
Trifoil 30°
|
0.0463 S
|
0.0062 S
|
|
10
|
3
|
-3
|
81/2 r3
cos 3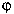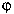
|
Trifoil 0°
|
0.0401 S
|
0.0062 S
|
|
11
|
4
|
0
|
51/2 (6r4
- 6r2 + 1)
|
Aberração esférica
|
0.0377 S
|
0.0024 S
|
|
12
|
4
|
2
|
A (4r4 - 3r2)
sin 2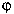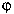
|
Astigmatismo 2a ord. 45°
|
---
|
---
|
|
13
|
4
|
-2
|
A (4r4 - 3r2)
cos 2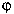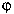
|
Astigmatismo 2a ord. 0°
|
---
|
---
|
|
14
|
4
|
-4
|
B r4 cos 4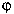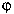
|
Tetrafoil 0°
|
---
|
---
|
|
15
|
4
|
4
|
B r4 sin 4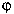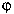
|
Tetrafoil 22.5°
|
---
|
---
|
Tab. 1: Polinômios de Zernike de 4th grau.
r = distância ao centro do círculo;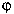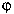
= ângulo azimutal; S = (D/ro)5/3.
Tilt (direção x)
|
Tilt (direção y)
|
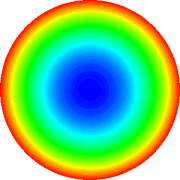
Defocus
|
Astigmatismo 1a ordem 0°
|
Astigmatismo 1a ordem 45°
|
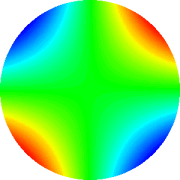
Coma (direção x)
|
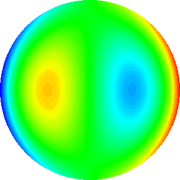
Coma (direção y)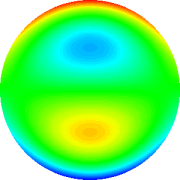
|
Trifoil 0°
|
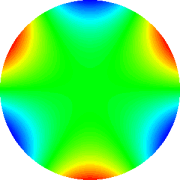
Trifoil 30°
|
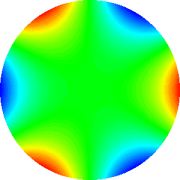
Aberração esférica
|
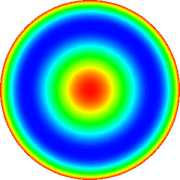
Tetrafoil 0°
|
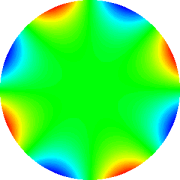
Tetrafoil 22.5°
|
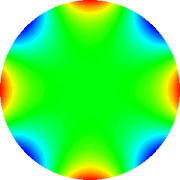
Astigmatismo 2a ordem 0°
|
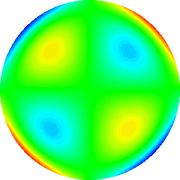
Astigmatismo 2a ordem 45°
|
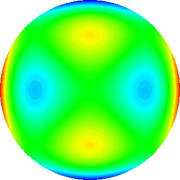
Tab. 2: Representação gráfica dos polinômios
de Zernicke de 4th grau
Voltar