with 
the angular frequency and t time, the wave equation
m
and dominate the degradation of spatial resolution. The spatial resolution
of the telescope is degraded to an order of magnitude greater than the
diffraction limit and the central intensity of a point source image is
degraded by two orders of magnitude. (Hubin & Noethe, 1993).
Turbulence is a non-linear process, and so the equations governing it are non-linear. In 1941, Kolmogorov attempted to model turbulence in the atmosphere using a statistical approach. The Kolomogorov theory of turbulence is based on the assumption that wind velocity fluctuations are approximately locally homogeneous and isotropic random fields for scales less than the largest wind eddies. (Beland, 1993; Beckers 1993).
How do phase variations due to atmospheric turbulence affect the intensity
of the incident electro-magnetic wave? Assuming the incoming electric field
portion of the electro-magnetic wave E is proportional to
with
the angular frequency and t time, the wave equation
reduces to
where k is the wavenumber for propagation in free space, n is the index
of refraction and the dispersion relation 
holds. (Note that the wavenumber for propagation through the atmosphere
is 
.)
This equation cannot be solved exactly, so we approximate the solution
using a perturbation expansion of n and E. This assumes that for the area
of the sky we are interested in, the index of refraction undergoes slow,
small perturbations due to the atmospheric turbulence. Let 
where 
is the incident electric field and 
is the scattered field. 
where 
.
Dropping the second order 
term,
Putting in the perturbation to E
Dropping the small 
term and using
equation 22 becomes
This can be solved in terms of
using Green's function for the wave equation, giving
integrating over the scattering volume between source and telescope.
(Beland, 1993).
However, this solution is only valid for very weak perturbations of
E and the integral over the scattering volume between the source and telescope
is not very convenient since the effects of phase variations are not obvious.
A less limiting method is the Rytov method of smooth perturbations. Here
E is written as
where 
and 
,
A is the amplitude and S is the phase of E. Lutomirski and Yura, using
an extended Huygens-Fresnel theory find
here integrating over a surface.
The intensity of the incoming wavefront will tell us how the phase fluctuations
degrade the resolution.
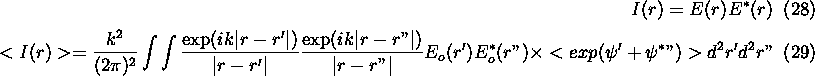
The mutual coherence function (MCF) in the focal plane of the telescope
is given by 
and is equal to 
where 
is the transverse coherence length. A spatially coherent wavefront will
have its spatial coherence degraded to
after passing through turbulence.
Most astronomical applications translate this spatial mutual coherence
function to the modulation transfer function (MTF) in the spatial frequency
domain. The modulation transfer function 
where f is the focal length, 
is the spatial frequency (cycles/length),
is the wavelength of light, and 
is the atmospheric coherence length or Fried parameter.
is about 10 cm for a vertical path for visible wavelength and characterizes
the effect of turbulence on the incoming wavefront. Since optical turbulence
blurs out point source functions, there is a cutoff spatial frequency 
and 
gives the limit of resolution due to optical turbulence. (Beland, 1993;
Beckers, 1993.)
The diffraction limit of resolution for 4m telescope at 500 nm is given
by equation 17
Assuming 
,
the angular resolution due to atmospheric turbulence R is
So turbulence in this case degrades the resolution by a factor of 100!
Voltar